پیوندگاه میانگین، میانه، ضریب چولگی و ضریب تغییرات در آمار

به گزارش حافظ خبر؛ از نخستین برون‌دادهای جدول فراوانی در دانش آمار، میانگین، میانه، مد، ضریب چولگی، ضریب تغییرات و پیوندهای آن‌هاست.
میانگین: ابتدا باید فراوانی را در مرکز دسته (مد) ضرب کرد. سپس همه مقادیر به دست آمده در هر طبقه را جمع کرده و در آخر تقسیم بر مجموع فراوانی‌ها کنیم و به این صورت میانگین تقریبی همه داده‌ها به دست می‌آید؛ یا همه داده‌ها را بهم می‌افزاییم و آنگاه بر تعداد آن‌ها بخش می‌کنیم.
میانه: اگر فراوانی زوج باشد، پس از مرتب شدن، دو عدد میانی فراوانی را جمع و تقسیم بر 2 می‌کنیم و اگر فرد باشد، عدد وسط میانه است.
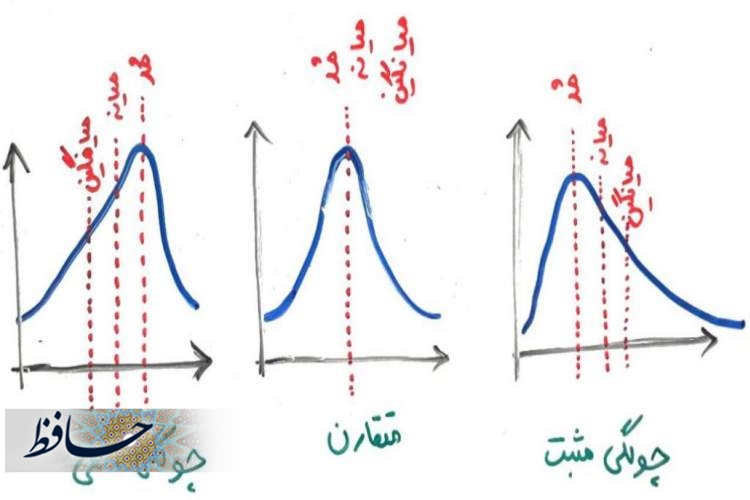
ضریب چولگی: چولگی را می‌توان کشش نمودار به یک سوی دانست پس اگر توزیع آماری متقارن باشد، چولگی صفر و اگر نامتقارن باشد، چولگی صفر نیست. اگر داده‌ها «یک نمایی» (Unimodal) باشند و دم منحنی توزیع احتمال به سوی راست باشد آن را چوله به راست و اگر به سوی چپ باشد چوله به چپ خوانده می‌شود.
ضریب چولگی اول پیرسون که در آن نما مبنا در نظر گرفته شده و انحراف میانگین از نما برحسب انحراف استاندارد محاسبه شده است:  Mean−Mode)/S)
ضریب چولگی دوم پیرسون اختلاف بین میانگین و میانه را مبنا قرار داده و نسبت آن را به انحراف استاندارد محاسبه می‌کند که گاه آن را «چولگی میانه پیرسون» (Pearson Median Skewness) نیز می‌نامند: (Mean−Median)3 بخش بر S؛
ضریب تغییرات: از آنجایی که کم بودن پراکندگی، نشانگر همگن بودن جامعه است، هر چه میزان ضریب تغییرات کمتر باشد، میانگین را معیار بهتری برای نقطه تمرکز می‌یابیم. بنابراین در بین دو جامعه، آن که دارای ضریب تغییرات کمتری باشد، جامعه بهتری بوده، زیرا نتایج گرفته شده از شاخص میانگین، دقت بیشتری دارند. از آنجایی که ضریب تغییرات بوسیله یک نسبت از کمیت‌های هم واحد، محاسبه و ساخته می‌شود، هیچ واحد اندازه‌گیری نداشته و به صورت درصدی مورد استفاده قرار می‌گیرد. همین موضوع نیز اهمیت استفاده از این شاخص را برای مقایسه بین جوامع مختلف، مشخص می‌کند. برای نمایش فرمول و رابطه محاسباتی ضریب تغییرات از علامت μ به عنوان میانگین و S برای انحراف معیار استفاده می‌کنند. در نتیجه محاسبه ضریب تغییرات به شکل زیر خواهد بود: CV=S/μ