جدول فراوانی و پیوند فراوانی، فراوانی نسبی، فراوانی تجمعی، فراوانی نسبی-تجمعی، دامنه تغییرات، فاصله طبقات، مُد، میانگین و میانه.
یادداشتی از محمدمهدی اسدزاده؛
ویژگیهای جدول فراوانی
تاریخ انتشارشنبه ۱ بهمن ۱۴۰۱ ساعت ۲۰:۲۲
به گزارش حافظ خبر؛ آمار، دانشی دادهگراست؛ با این بار که دانش آمار، در هر زمینهای که بیان شود، در گام نخست، بایستی دادهها نیاز را شناسایی و سپس به گردآوری و برپایه نیاز، دستهبندی تا با بررسی آنها، به بروندادی نیاز خود برسیم.
جدول فراوانی: دادهها پس از گردآوری، دستهبندی و در جدولی به نام جدول فراوانی، کنار هم چینش میشوند. جدول فراوانی نشاندهنده پراکندگی دادهها و ویژگیهای متغیرهای کمی و کیفی مانند میانگین، میانه و نما است. همچنین در راستای شاخصهای مرکزی (central Index)، شاخص پراکندگی (Dispersion Index) و مقایسه گروهی دادهها با گروههای دیگر برای استنباط آماری ساخته میشود.
جدول فراوانی: دادهها پس از گردآوری، دستهبندی و در جدولی به نام جدول فراوانی، کنار هم چینش میشوند. جدول فراوانی نشاندهنده پراکندگی دادهها و ویژگیهای متغیرهای کمی و کیفی مانند میانگین، میانه و نما است. همچنین در راستای شاخصهای مرکزی (central Index)، شاخص پراکندگی (Dispersion Index) و مقایسه گروهی دادهها با گروههای دیگر برای استنباط آماری ساخته میشود.
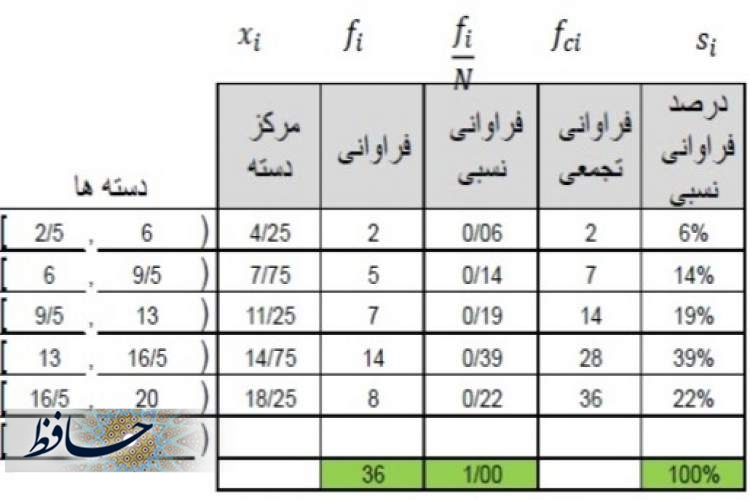
| ده یا حدود رده (طبقات) | فراوانی- f | فراوانی نسبی- r | فراوانی تجمعی- F | فراوانی نسبی-تجمعی- R |
| جمع |
به تعداد تکرارهای هر مقدار از ستون رده یا گستره رده، «فراوانی» (Frequency) میگویند. مجموع ستون فراوانی برای همه ردهها برابر با تعداد نمونه یا مشاهدات (n) خواهد بود. فراوانی مربوط به رده iام را با fi نشان میدهیم.
فراوانی نسبی: اگر فراوانی هر رده را به جمع فراوانیها تقسیم کنیم، «فراوانی نسبی» (Relative Frequency) بهدست میآید. میتوان مقدار این ستون را به صورت درصدی نیز نمایش داد. نماد مربوط به فراوانی نسبی رده i ام، به صورت ri است. پس: ri=fi/n که جمع ستون فراوانی نسبی برابر با ۱ و در حالتی که مقدارهای آن به صورت درصدی باشند برابر با ۱۰۰٪ خواهد بود.
فراوانی تجمعی: برای محاسبه «فراوانی تجمعی» (Cumulative Frequency) برای هر رده، کافی است فراوانی آن رده را با فراوانی ردههای قبلی جمع کرد. فراوانی تجمعی رده iام را با Fi نشان میدهیم؛ پس خواهیم داشت: Fi=∑fk که k از 1 تا i خواهد بود.
به منظور افزایش سرعت در انجام محاسبه فراوانی تجمعی برای یک رده، کافی است فراوانی تجمعی رده قبلی را با فراوانی رده مورد نظر جمع کرد.
فراوانی نسبی-تجمعی: ستون «فراوانی نسبی-تجمعی» (Cumulative Relative Frequency) درست به مانند ستون فراوانی تجمعی، از حاصل جمع فراوانی نسبی ردههای قبلی و رده انتخابی ایجاد میشود.
دامنه تغییرات: از تفاضل بزرگترین عدد از کوچکترین عدد به اضافه یک به دست آورد: R=X2-X1+1
فاصله همه طبقات در یک جدول توزیع فراوانی با هم برابر است:
تعداد طبقات (K) / دامنه تغییرات (R) = فاصله طبقات (I)
مد: 2/(حد پایین طبقه + حد بالای طبقه) = Xc
مد در طبقهبندی: به طبقهای که بیشترین فراوانی را دارد، طبقه مد گویند. Xc=L+(d1/(d1+d2))i که در آن L حد پایین طبقه مد، d1 اختلاف تا طبقه پسین، d2 اختلاف تا طبقه پیش و i فاصله طبقه مد است.
میانگین: ابتدا باید فراوانی را در مرکز دسته (مد) ضرب کرد. سپس تمام مقادیر به دست آمده در هر طبقه را جمع کرده و در آخر تقسیم بر مجموع فراوانی ها کنیم و به این صورت میانگین تقریبی همه داده ها به دست می آید.
میانه: اگر فراوانی زوج باشد، پس از مرتب شدن، دو عدد میانی فراوانی را جمع و تقسیم بر 2 میکنیم و اگر فرد باشد، عدد وسط میانه است.
مولف : محمدمهدی اسدزاده
کد مطلب : ۲۶۸۶۷